GAN, Generative Adversarial Nets

본 포스트는 딥러닝을 활용해 센세이션을 일으킨 Generative Model, GAN 논문을 정리한 것입니다. 2014년 NIPS에 억셉된 후 어마어마하게 발전된 개념이지요. 공부한 내용을 정리하는 것이기에 잘못된 점이 있을 수 있습니다. 해당 내용에 대한 교정, 첨언, 조언은 언제나 환영합니다.

GAN의 컨셉

GAN은 Generative Adversarial Nets의 앞글자를 따 만들어진 단어로 이름에서 그 특징이 잘 나타나 있습니다. 생성 모델이며(generative), 적대적인 방법으로 학습하는(adversarial), 네트워크(nets)란 뜻입니다. 각 단어들이 뜻하는 것을 하나씩 살펴보겠습니다.

우선 GAN은 생성 모델을 만드는 것이 최종 목적인 알고리즘입니다. 학습하려는 데이터의 분포를 $p_{x}$ 또는 $p_{data}$라고 표현합니다. 특정 모델이 이 분포를 잘 모방하는 $p_g$ 분포를 만들어낼 수 있다면 이 모델을 생성 모델이라고 합니다. 그러면 이 생성 모델을 어떻게 만들 수 있을까요?

생성 모델을 만들기위해 제안된 프레임워크가 GAN 논문의 가장 큰 contribution입니다. 그리고 이 프레임워크를 잘 설명하는 단어가 Adversarial 입니다. 이 과정에는 크게 두 모델이 필요합니다. 하나는 생성 모델 generator이고 다른 하나는 판별 모델 discriminator 입니다. 앞으로 generator은 G로 discriminator은 D로 표현하겠습니다. G가 하는 일은 학습 데이터 $p_{x}$를 모방하여 데이터를 생성해내는 것이고, D가 하는 일은 G가 생성한 데이터를 판단하는 것입니다. G는 D가 제대로 판단하지 못하도록 그럴듯한 데이터를 점차 잘 생성해내고, D는 생성된 데이터가 $p_{x}$와 유사한지 판단하지요. 이렇게 G와 D는 서로 대결하는 구도를 통해 성능을 높여갑니다. 충분히 학습이 이루어져 G가 D를 속일 수 있는 수준이 된다면 이는 곧 $p_{g}$ 분포가 $p_{x}$ 분포를 잘 모방했다는 의미로 우리가 원하는 생성 모델이 만들어 진 것입니다.

마지막으로 nets은 위에서 설명한 G와 D를 딥러닝 아키텍쳐로 구성했다는 뜻입니다. 딥러닝은 데이터 수가 많고 고차원일 때 내재된 특징을 잘 찾아내는 능력으로 각광받고 있는 머신러닝 알고리즘입니다. 특히 딥러닝은 SGD 방식으로 쉽게 학습시킬 수 있다는 특징이 있습니다. GAN 프레임워크를 구성하는 G와 D가 딥러닝 아키텍쳐로 구성되었기에 고차원 데이터 분포 $p_{x}$의 특징을 잘 찾아내 모방할 수 있을 뿐더러 SGD 방식으로 학습시키는 것도 가능합니다.

핵심 목적 함수

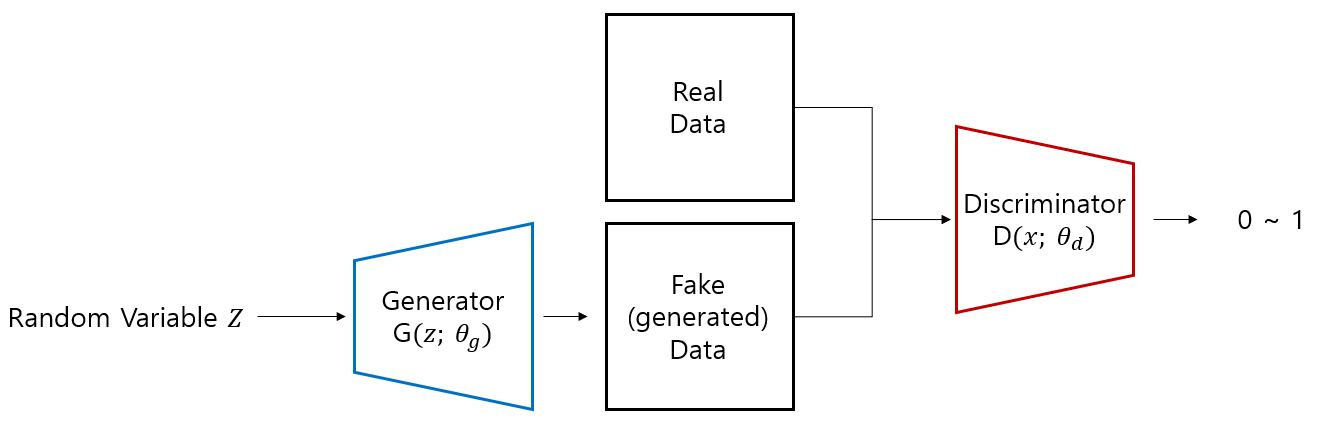
위의 그림은 GAN의 전체 프레임워크를 나타낸 그림입니다. 이제부터는 수식을 포함하여 이 프레임워크를 좀 더 자세히 살펴보겠습니다. 먼저 GAN의 목적 함수(objective function)는 아래와 같습니다.

이 수식에서 $p_{data}$는 학습 데이터 셋을 의미하고 $p_{z}$는 임의의 확률 분포를 의미합니다. G는 $p_{z}$에서 샘플링 된 랜덤한 노이즈 벡터 z를 입력으로 받아 학습 데이터와 유사한 데이터를 생성합니다. 이렇게 만들어진 데이터를 $G(z)$ 또는 $G(z, \theta_{g})$라고 합니다. D는 $G(z)$와 $p_{data}$에서 샘플링 된 학습 데이터 x를 입력으로 받아 0~1 사이의 확률 값을 결정합니다.

G와 D는 목적 함수 $V(G,D)$를 바라보는 방향이 다릅니다. 그렇기 때문에 수식을 G의 관점과 D의 관점에서 다르게 해석할 필요가 있습니다. 두 관점을 구분해서 자세히 살펴보겠습니다.

G의 관점

G의 목적은 $V(G,D)$를 최소화시키는 것입니다.

G의 관점에서 저 수식이 최소화된다는 것은 곧 G가 $p_{data}$를 모방하는 $p_{g}$를 잘 만들어낸다는 뜻이기 때문입니다.

G는 $p_{z}$에서 샘플링 된 랜덤한 노이즈 벡터 z를 입력으로 받아 $G(z)$를 생성합니다. 만약 $G(z)$가 $p_{data}$에서 샘플링 된 x와 유사하다면 D는 1에 가까운 확률 값을 반환할 것입니다. $V(G,D)$의 구성요소 중 G와 관련이 있는 것은 두번째 term $E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$ 입니다. $G(z)$가 D를 통해 1에 가까운 확률 값을 반환받는다면 괄호안의 log 수식은 $\log (1-1)$에 가까운 값이 되어 마이너스 무한대에 가까워집니다. 즉, 목적 함수 $V(G,D)$는 굉장히 작은 값을 가지게 되겠지요. 결과적으로 G가 학습 데이터를 잘 모방할수록 $V(G,D)$는 작아지게 됩니다.

D의 관점

G와는 반대로 D는 $V(G,D)$가 최대화되길 바랍니다.

D는 주어진 데이터가 $p_{data}$온 것인지 $p_{g}$에서 온 것인지를 잘 구별하는 것을 목적으로 하기 때문입니다.

D는 입력받은 데이터가 학습 데이터에서 온 경우 1에 가까운 값을 반환하도록 학습됩니다. 이는 $V(G,D)$의 첫번째 term $E_{x \sim p_{data}(x)}[\log D(x)]$이 0에 가까워짐을 나타냅니다. $D(x)$가 [0,1] 범위를 가지기 때문에 0에 가까워진다는 것은 곧 최대값에 가까워진다는 것을 의미하지요.

두번째로 D는 G에서 온 데이터는 0에 가까운 값을 반환하도록 합니다. 이는 $V(G,D)$의 두번째 term $E_{z \sim p_{z}(x)}[\log (1-D(G(z)))]$ 또한 0에 가까워진다는 것을 의미합니다. 이것또한 최대값에 근접하게 된다는 것이네요. 결과적으로 D는 목적 함수 $V(G,D)$를 최대화시키게 됩니다.

Framework 동작 방식

지금까지 핵심 목적 함수와 이를 바라보는 G, D의 관점을 살펴보았습니다. 이제는 전체 프레임워크에서 G와 D가 어떻게 상호작용하여 성능을 높여가는지 보겠습니다. 이는 GAN 논문의 figure 1과 algorithm 1에 자세히 설명되어 있습니다.

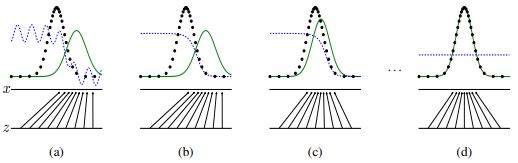
먼저 GAN 논문의 figure 1을 보겠습니다. 이 그림은 어느정도 학습이 진행된 G와 D를 나타냅니다. 임의의 z 공간에서 샘플링 된 샘플들은 z 실선에서 x 실선으로 매핑되는 화살표입니다. 이 화살표가 x 실선의 어떤 점으로 매핑되는지를 나타내는 게 $G(z, \theta_{g})$ 입니다. 이렇게 매핑된 점들의 분포 $p_g$를 나타내는 것이 초록 실선입니다. 검은 점선은 학습 데이터 분포 $p_{data}$를 의미하고 D의 분포는 파란 점선입니다.

(a)는 G 네트워크가 학습되어 $p_{data}$분포를 일부 모방한 상태를 의미합니다. 이후 (b)는 목적 함수를 최대화하도록 D를 학습한 결과입니다. 이 과정을 통해 구불구불한 파란색 선이 매끄러워 짐을 확인할 수 있습니다. 특히 G의 분포가 학습 데이터 분포를 정확히 따라가는 왼쪽 분포에서 D(x)는 $\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$로 수렴하게 됩니다. (c)는 (b)의 단계에서 G를 다시 학습시킨 결과입니다. G의 분포가 학습 데이터 분포를 더 잘 따라가는 것을 확인할 수 있습니다. 이 과정을 반복해서 G와 D가 점차 업데이트되고 GAN이 최종적으로 도달하기 바라는 결과가 (d)입니다.

figure 1 과정을 pseudocode로 표현한 것이 위 그림입니다. 전체 학습 iteration에서 목적 함수를 따라 D를 k번 학습시키고 G를 한 번 학습시킵니다. D를 학습할 때는 z 분포에서 샘플링 된 m개 데이터 z와 학습 데이터 분포에서 샘플링 된 m개 데이터 x를 사용합니다. 그리고 G를 학습할 때는 z 분포에서 샘플링 된 m개 데이터 z를 사용합니다.

GAN을 학습할 때 optimal D가 미리 주어지면 G는 적절한 gradient를 받기 어렵습니다. 학습 초반에 G가 만들어내는 데이터는 아직 실제 데이터와 차이가 있고 D는 쉽게 0에 가까운 확률 값을 반환하기 때문입니다. 이는 G에게 충분한 gradient가 전달되지 못한다는 의미이기도 합니다. 그래서 트릭으로 $log(1-D(G(z)))$를 최소화하는 것보다 $log(D(G(z)))$를 최대화하는 방법이 있습니다. 이를 그림으로 살펴보겠습니다.

GAN의 학습 초반에 G가 D로부터 낮은 확률 값 0.1~0.2 정도의 값을 반환받는다면 $log(1-x)$의 평균 기울기는 약 -1.18이 되고 $log(x)$의 평균 기울기는 약 6.93이 됩니다. 같은 목적 함수라도 $log(D(G(z)))$가 더 많이 G를 업데이트 시킬 수 있는 것입니다. 이런 이유로 논문에서는 $log(D(G(z)))$를 최대화하는 트릭을 언급합니다. 이처럼 GAN은 G와 D가 적절한 성능을 내도록 밸런스를 잡아줄 필요가 있습니다.

이론적 background

Adversarial framework를 따라 무한한 capacity를 가진 non-parametric 모델 G, D가 점차 성능을 높여가서 결국에는 $p_{g}$가 $p_{data}$에 수렴하게 된다는 이론적 배경을 살펴보겠습니다.

[Proposition 1]

G가 주어졌을 때, 최적의 D는 $D_G^* (x) = \frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$ 이다.

[Proof]

G가 주어졌을 때, D를 학습하는 기준은 $V(G,D)$ 수식이 최대가 되는 것입니다.

이 수식은 $p_{data}$와 $p_{g}$가 정의되는 구간에서만 계산되면 됩니다. 이를 논문에서는 $Supp(p_{data}) \cup Supp(p_{g})$로 표현합니다(지지집합이라는 개념으로 해당 함수가 0이 아닌 점들의 집합을 의미합니다). 즉, $p_{data}$가 0이 아니고 $p_{g}$가 0이 아닌 모든 공간을 의미합니다. $V(G,D)$ 수식은 $a \log (y) + b \log (1-y)$ 꼴로 나타낼 수 있는데 a와 b가 0이 아니고 y가 [0,1] 구간에 있다는 조건하에서, $y=\frac{a}{a+b}$인 지점에서 최대값을 갖습니다. D가 최적화 된 $D_G^*$을 $V(G,D)$에 대입하여 다시 표현한 수식을 논문에서는 C(G)라고 표현합니다.

[Theorem 1]

$p_{g}=p_{data}$일 때, 임의의 학습 기준 C(G)는 전역 최저점(global minimum)에 도달하고 그 값은 $- \log 4$다.

[Proof]

$p_{g}(x) = p_{data}(x)$이면 $D_G^* (x)=\frac{1}{2}$가 됩니다. 이 값을 C(G)에 대입하면 $\log \frac{1}{2} + \log \frac{1}{2} = -\log 4$를 얻을 수 있습니다. 그러나 이 값은 $p_{g}$와 $p_{data}$ 분포가 일치할 때 얻어지는 것으로 분포의 차이가 존재할 경우 패널티가 붙어야 합니다. C(G)를 변형하는 과정을 통해 중간에 어떤 패널티가 생길 수 있는지 살펴보겠습니다.

KL은 Kullback-Leibler divergence의 약자로 두 분포의 차이를 설명하는 개념입니다. 임의의 두 분포 P와 Q가 있을 때, 다음과 같은 수식으로 표현됩니다.

만약 P와 Q가 동일한 분포라면 KL divergence는 0 값을 가지게 됩니다. 동일한 분포가 아니라면 양수 값을 나타나게 되고 이는 최소점 $-\log 4$에 더해져 패널티 역할을 하게 되는 것입니다. 추가적으로 두 KL divergence는 Jensen-Shannon divergence로 변환이 가능합니다. Jensen-Shannon divergence는 아래와 같은 수식으로 표현됩니다.

논문에 있는 수식 (5)와 (6)은 위의 과정에 따라 유도되고 $p_{g}$와 $p_{data}$ 분포가 동일하다면 최소값 $-\log 4$를 갖게 됩니다.

[Proposition 2]

충분한 capa를 가진 G와 D가 algorithm 1을 따라 학습하면 최종적으로 $p_{g}$는 $p_{data}$에 수렴한다.

[Proof]

$V(G,D)$를 $U(p_{g},D)$라는 $p_{g}$의 convex 함수로 가정합니다. Convex 함수의 supremum의 subderivatives라는 표현은 해당 함수에서 얻을 수 있는 모든 기울기 집합을 의미합니다(supremum, subderivatives). 그리고 이 집합 안에는 함수의 최대값이 되는 지점의 기울기도 포함되어 있습니다. 이를 논문에서는 다음과 같은 수식으로 표현합니다.

이는 최대 지점으로 미분해서 G를 업데이트 할 수 있다는 뜻이고 결국 SGD로 딥러닝 모델을 학습할 수 있다는 개념과 동치입니다. 앞선 명제들과 합쳐 G가 주어졌을 때 최적 D를 찾을 수 있고 또 D가 주어지면 최적 G를 찾아갈 수 있으니 결국 algorithm 1에 따라 $p_{g}$는 $p_{data}$에 수렴하게 됩니다. 단, proposition 2 명제에서 나타난 논리적 아쉬움은 해당 증명에서 얻어진 gradient는 $p_{g}$에 관한 것이나 실제 모델을 학습시키는 대상은 G 모델의 $\theta_{g}$입니다. 이런 이론적 보장에 대한 아쉬움을 논문에서도 언급하고는 있지만 그럼에도 GAN framework는 유효하며 합리적으로 모델이 데이터 분포를 학습할 수 있습니다.

결과

GAN은 적대적 프레임워크를 통해 학습 데이터 분포를 잘 모방하는 G를 만들어내는 것이 목적입니다. 그러나 얼마나 잘 만들어냈는지를 정량적으로 평가하는 것은 매우 어렵습니다. 평가 지표를 정의하기 어렵고 생성된 데이터가 해당 분포에서 나오는 것이 자연스러운 것인지 학습이 덜 된 것인지 판단하기 어렵기 때문입니다. 또한 주어진 테스트 데이터셋도 G를 직접적으로 평가하는데 사용할 수 없는 문제도 있습니다. 그래서 정성적으로 생성된 데이터를 보고 판단하는 경우가 있는데 이미지 데이터의 경우 이런 판단하기가 좋습니다.

가장 오른쪽 그림은 생성된 이미지와 가장 인접한 학습 데이터셋을 뽑은 것입니다. 생성된 이미지가 그럴듯한 이미지를 생성해냈는지, 그리고 학습 데이터와 유사한 의미를 지닌 이미지를 생성했는지 정성적으로 판단할 수 있을 것입니다.

수치적으로 GAN의 성능을 파악하기 어렵지만 이 프레임워크를 통해 우린 딥러닝 기반의 생성 모델을 얻을 수 있습니다. 특히, 명시적으로 특정 분포를 설정하지 않고 데이터 분포를 모방하는 이 방식은 학습 데이터 분포가 다소 난해하더라도 잘 모방할 수 있다는 장점이 있습니다.