오차의 최소화, Gradient Descent
11 Apr 2019 |딥러닝에서 사용되는 최적화 방법론인 gradient descent에 관한 내용입니다. 이 분야를 공부하는 사람이라면 누구나 다 알고 있는 내용이지만 그래도 한 번 정리하여 개념이 흔들릴 때 참고하고자 합니다. 이 포스트가 누군가에게 도움이 되기를 바라고 혹시 잘못된 내용이 있다면 첨언해 주시길 부탁드립니다. 포스팅 작성에 도움을 받은 참고 위키독스와 위키피디아, 블로그는 링크를 걸어두었습니다.
what is the gradient?
다변수 함수 $f$가 $n$개 변수로 이루어져 있다면 다음과 같이 표현할 수 있습니다.
\[f(x_1, x_2, ..., x_n)\]이 때 그래디언드(gradient)는 함수 $f$를 각 변수로 편미분(Partial derivative)한 값을 원소로 하는 벡터라고 정의할 수 있습니다.
\[\nabla f=(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n})\]이 벡터는 기울기가 가장 가파른 곳으로의 방향, $f$값이 가장 가파르게 증가하는 방향을 의미합니다.
예를 들어, $f(x, y) = x^2 + y^2 + xy$라고 하면 그래디언트는 $\nabla f=(2x+y, 2y+x)$입니다. 임의의 점 $(1, 3)$에서 함수 $f$ 값이 최대로 증가하는 방향은 $(5, 7)$이고 그 기울기(벡터의 크기, 증가의 가파른 정도)는 $\lVert (5, 7) \rVert = \sqrt{5^2 + 7^2} = \sqrt{74}$입니다.
gradient method
그래디언트는 함수값을 최대화시키는 방향을 의미한다는 점을 위에서 이야기했습니다. 그래디언트 방향을 반대로 하면 어떻게 될까요? 함수값을 최소화시키는 방향을 나타내게 될 것입니다. 이 방향으로 나아가 최적값을 찾는 방법론을 우리는 gradient method라고 부릅니다. 많은 문제의 해답을 이 gradient method로 찾는 이유는 세상에 존재하는 많은 문제들이 analytic하게 답을 구하기 쉽지 않아 점진적으로 문제를 풀어나가야 하며 그 방식에 알맞는 알고리즘이기 때문입니다. 수식으로 알고리즘을 좀 더 살펴보겠습니다.
\[x_{n+1} = x_n - \alpha \nabla_x f\]$x_{n+1}$은 $x_n$에서 일정 값을 뺀 결과임을 수식에서 확인할 수 있습니다. 우선 각 요소를 살펴보면 $\nabla_x f$는 함수 $f$를 변수 $x$로 편미분한 값이고 $\alpha$는 learning rate입니다. 전체 함수값을 최소화시키기 위해 $x$의 변화량을 나타내는 것이 $\nabla_x f$이고 그 비율을 조절하는 역할이 learning rate입니다. Learning rate를 조절해서 변수 $x$가 급격하게 변해 optimal point를 지나치는 것을 방지할 수 있습니다. 현재 위치에서 그래디언트 반대 방향(음수 방향)으로 함수를 업데이트 했기 때문에 전체 함수는 최소값을 찾아가게 됩니다. 만약 함수 최대값을 찾아가기 위해 gradient ascent방법론을 수행하고자 한다면 다음과 같은 수식을 활용하면 됩니다.
\[x_{n+1} = x_n + \alpha \nabla_x f\]다만 주어진 그래디언트가 양수, 음수인지에 따라 값은 얼마든지 반전될 수 있기 때문에 통칭해서 gradient method라고 불러도 무방합니다. 여기까지 어떻게 그래디언트 값을 활용해서 변수값을 업데이트 하는지 확인했습니다. 그러나 무한정 학습하는 것은 아닙니다. Gradient method 방법은 점진적으로 해를 찾아가는 numerical, iterative 방식이기 때문에 어느 시점에서 학습을 멈춰야합니다. 또 때로는 예기치 못하게 발산할 가능성도 있습니다. 따라서 다음과 같은 조건을 만족할 경우에만 변수를 업데이트하고 학습을 진행합니다.
\[L(\theta + \nabla \theta) < L(\theta)\]업데이트 된 변수를 기반으로 구한 함수 $L$이 업데이트 되기 이전의 변수로 구한 함수값보다 작은 경우에만 변수를 업데이트 합니다(gradient descent의 경우). 아래 코드는 gradient descent방법론이 최적해를 찾아가는 과정입니다.
(x, y) = (10, 21)
init_m = 3
init_b = 2
lr = 0.01
y_hat = init_m * x + init_b
new_m = 3
new_b = 2
for i in range(20):
tmp_m = new_m - lr * x
tmp_b = new_b - lr * 1
tmp_y_hat = tmp_m * x + tmp_b
print("iter :", i , ", y_hat :", y_hat, ", tmp_y_hat :", tmp_y_hat)
if (y-y_hat)**2 > (y-tmp_y_hat)**2:
new_m = tmp_m
new_b = tmp_b
y_hat = new_m * x + new_b
print("(init_m, init_b) :", (init_m, init_b), ", (new_m, new_b) :", (new_m, new_b))
######################################################################
iter : 0 , y_hat : 32 , tmp_y_hat : 30.99
iter : 1 , y_hat : 30.99 , tmp_y_hat : 29.98
iter : 2 , y_hat : 29.98 , tmp_y_hat : 28.969999999999995
iter : 3 , y_hat : 28.969999999999995 , tmp_y_hat : 27.959999999999997
iter : 4 , y_hat : 27.959999999999997 , tmp_y_hat : 26.949999999999996
iter : 5 , y_hat : 26.949999999999996 , tmp_y_hat : 25.939999999999994
iter : 6 , y_hat : 25.939999999999994 , tmp_y_hat : 24.929999999999993
iter : 7 , y_hat : 24.929999999999993 , tmp_y_hat : 23.919999999999995
iter : 8 , y_hat : 23.919999999999995 , tmp_y_hat : 22.909999999999993
iter : 9 , y_hat : 22.909999999999993 , tmp_y_hat : 21.89999999999999
iter : 10 , y_hat : 21.89999999999999 , tmp_y_hat : 20.88999999999999
iter : 11 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 12 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 13 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 14 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 15 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 16 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 17 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 18 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
iter : 19 , y_hat : 20.88999999999999 , tmp_y_hat : 19.87999999999999
(init_m, init_b) : (3, 2) , (new_m, new_b) : (1.899999999999999, 1.89)
######################################################################
backpropagation
Backpropagation 알고리즘은 역전파라고 불리는 알고리즘입니다. 특정 작업을 수행하는 함수가 존재할 때, 해당 함수에 있는 파라미터값을 효과적으로 학습하는 반복적이고 재귀적인 알고리즘이라고 할 수 있습니다. 저는 평소에 딥러닝에 관심을 가지고 있기에 간단한 모델 예시를 통해 backpropagation 알고리즘을 알아보도록 하겠습니다.
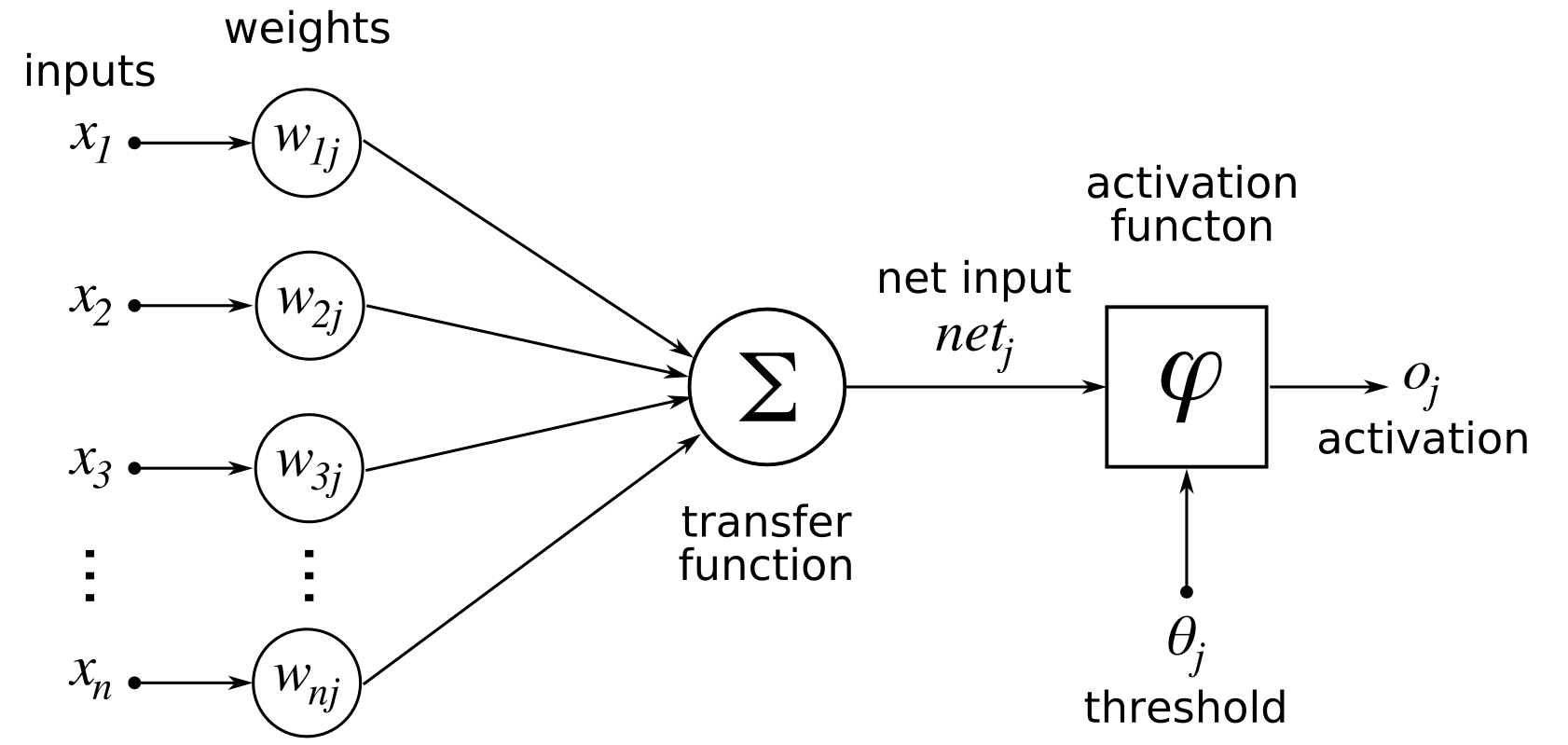
해당 모델은 $x_1$부터 $x_n$까지 n개 입력값을 받아 $o_j$라는 결과값을 반환하는 함수입니다. 그리고 이 결과값을 내는데 사용되는 파라미터는 $w_{1j}$부터 $w_{nj}$까지 n개입니다. 파라미터와 입력값을 서로 곱해서 transfer function을 통해 그 합을 구하고 결과값 ${net}_j$를 얻습니다. 이 과정을 element-wise sum이라고 부르기도 합니다. 이 ${net}_j$를 특정 activation function에 입력값으로 주어 최종 결과물인 $o_j$를 반환하게 됩니다.
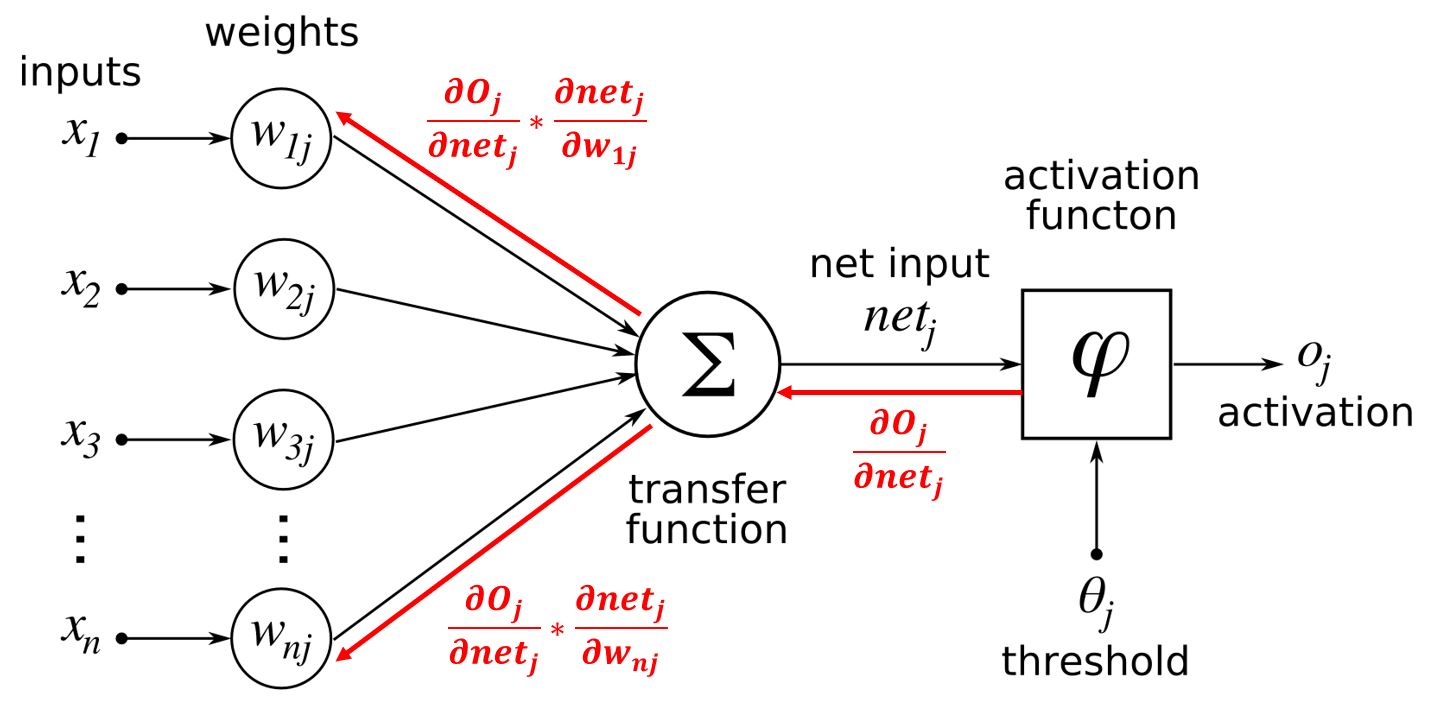
자 그러면 이제부터 backpropagation을 살펴보겠습니다. 해당 함수는 입력 $x$를 받아 결과 $o$를 반환하는데 이 결과가 특정 값에 가까워지기를 원한다고 하겠습니다. 그러나 랜덤한 값으로 초기화 된 $w$ 값으로부터는 원하는 결과를 얻지 못할 확률이 큽니다. 때문에 해당 값에 가까워 질 수 있도록 $w$값을 조절하는 알고리즘에 gradient method, backpropagation이 사용됩니다. 현재의 $w_{1j}$가 $o_j$에 미치는 영향도, 순간 기울기, 편미분 값은 $\frac{\partial {o_j}}{\partial w_{1j}}$입니다. Gradient method 수식에 따르면 원하는 결과값 $o_j$를 얻기 위해 $w_{1j}$를 업데이트 하는 수식은 $w_{1j_{n+1}} = w_{1j_{n}} - \alpha \frac{\partial {o_j}}{\partial w_{1j}}$입니다. 해당 수식서 $\frac{\partial {o_j}}{\partial w_{1j}}$ 부분은 chain rule을 통해 여러 단계로 분할하는 것이 가능합니다. 위 모델 그래프 구조에 따라 $\frac{\partial {o_j}}{\partial w_{1j}} = \frac{\partial {o_j}}{\partial {net_j}} \frac{\partial {net_j}}{\partial w_{1j}}$로 분할이 가능합니다. $\frac{\partial {o_j}}{\partial {net_j}}$와 $\frac{\partial {net_j}}{\partial w_{1j}}$은 local gradient라고 불립니다. 각 단계의 local gradient값을 구해서 그 값을 모델의 결과로부터 입력값까지 전파시켜가는 이 과정을 backpropagation 알고리즘이라고 부릅니다. 아래 그림처럼 진행됩니다.
pytorch backpropagation example
딥러닝 툴인 pytorch를 이용해 backpropagation 과정에서 gradient가 전파되는 과정을 한 번 살펴보겠습니다. 이 섹션을 작성하는 데 참고한 사이트는 링크를 걸어두었습니다. 먼저 역전파를 수행할 간단한 딥러닝 모델을 만들겠습니다. 코드와 그림은 다음과 같습니다.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(2,2)
self.s1 = nn.Sigmoid()
self.fc2 = nn.Linear(2,2)
self.s2 = nn.Sigmoid()
self.fc1.weight = torch.nn.Parameter(torch.Tensor([[0.15,0.2],[0.25,0.30]]))
self.fc1.bias = torch.nn.Parameter(torch.Tensor([0.35]))
self.fc2.weight = torch.nn.Parameter(torch.Tensor([[0.4,0.45],[0.5,0.55]]))
self.fc2.bias = torch.nn.Parameter(torch.Tensor([0.6]))
def forward(self, x):
x= self.fc1(x)
x = self.s1(x)
x= self.fc2(x)
x = self.s2(x)
return x
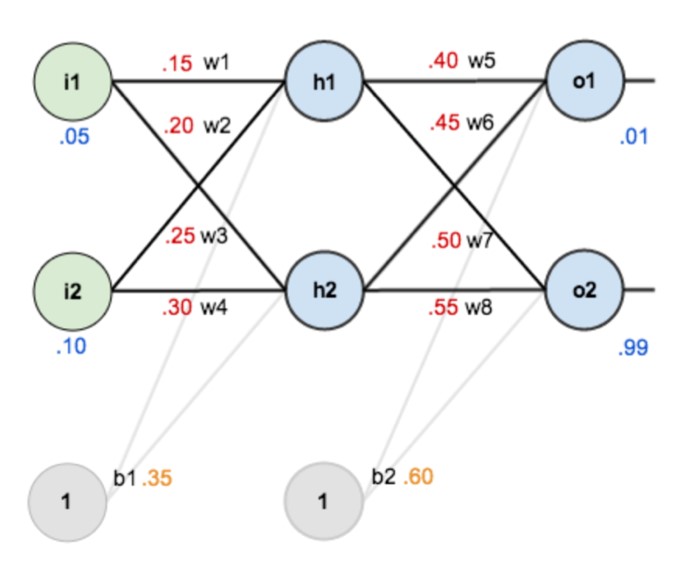
간단한 ANN 모델입니다. 히든 레이어 2개를 가지고 있고 그 크기는 2로 동일하며 activation function으로는 시그모이드(sigmoid function)을 사용했습니다. 첫번째 히든레이어의 가중치는 [[0.15,0.2],[0.25,0.30]], [0.35] 값을 가지고 있고 두번째 히든레이어의 가중치는 [[0.4,0.45],[0.5,0.55]], [0.6] 값을 가지고 있습니다. 이런 형태를 가진 ANN 모델에 [0.05, 0.1]을 입력으로 줄 경우 어떤 forward path와 backward path값이 나타나는지 확인해 보겠습니다.
class Hook():
def __init__(self, module, backward=False):
if backward==False:
self.hook = module.register_forward_hook(self.hook_fn)
else:
self.hook = module.register_backward_hook(self.hook_fn)
def hook_fn(self, module, input, output):
self.input = input
self.output = output
def close(self):
self.hook.remove()
net = Net()
hookF = [Hook(layer[1]) for layer in list(net._modules.items())]
hookB = [Hook(layer[1],backward=True) for layer in list(net._modules.items())]
data = torch.Tensor([0.05,0.1])
out=net(data)
out.backward(torch.tensor([1.,1.]))
print('***'*3+' Forward Hooks Inputs & Outputs '+'***'*3)
for hook in hookF:
print(hook.input)
print(hook.output)
print('---'*17)
print('\n')
print('***'*3+' Backward Hooks Inputs & Outputs '+'***'*3)
for hook in hookB:
print(hook.input)
print(hook.output)
print('---'*17)
먼저 forward path를 살펴보겠습니다. Pytorch가 제공하는 함수중에는 register_forward_hook가 있습니다. 이를 사용하면 네트워크를 구성하는 각 모듈의 입력값과 출력값을 확인할 수 있고 내부 동작을 변경할 수도 있습니다. 현재 코드에서는 입력과 출력값이 무엇인지 확인하는 용도로 코드가 작성되었습니다. 결과를 확인해 보겠습니다.
********* Forward Hooks Inputs & Outputs *********
(tensor([0.0500, 0.1000]),)
tensor([0.3775, 0.3925], grad_fn=<AddBackward0>)
---------------------------------------------------
(tensor([0.3775, 0.3925], grad_fn=<AddBackward0>),)
tensor([0.5933, 0.5969], grad_fn=<SigmoidBackward>)
---------------------------------------------------
(tensor([0.5933, 0.5969], grad_fn=<SigmoidBackward>),)
tensor([1.1059, 1.2249], grad_fn=<AddBackward0>)
---------------------------------------------------
(tensor([1.1059, 1.2249], grad_fn=<AddBackward0>),)
tensor([0.7514, 0.7729], grad_fn=<SigmoidBackward>)
---------------------------------------------------
첫 히든레이어로 들어간 입력값은 [0.05, 0.1] 이었습니다. 그리고 이것이 가중치 [[0.15,0.2],[0.25,0.30]]과 행렬 곱셈(matrix multiplication)을 수행하고 bias인 [0.35]와 더해진 결과가 [0.3775, 0.3925]입니다. 계산 수식은 [(0.05 * 0.15) + (0.1 * 0.2) + 0.35, (0.05 * 0.25) + (0.1 * 0.3) + 0.35]처럼 진행된 것입니다. 두번째 결과는 시그모이드 함수에 이전 레이어의 결과값 [0.3775, 0.3925]을 입력으로 준 것입니다. 시그모이드 함수 수식은 $ \frac{1}{1+exp(-x)} $입니다. 여기에 이전 결과값을 대입하면 [0.5933, 0.5969] 결과값을 얻을 수 있습니다. 나머지 과정은 동일합니다.
다음은 backward path 과정을 보겠습니다. Forward에 비해 수식이 조금 복잡해졌지만 하나하나 따라가보면 그리 어렵지않게 이해할 수 있습니다. 먼저 out.backward(torch.tensor([1.,1.])) 함수는 결과값이 2개고 두 결과값으로부터 gradient backpropagation을 수행한다는 함수로 이해할 수 있습니다. 흘러들어오는 그래디언트가 1이라고 지정해주는 함수로 봐도 무방합니다. 보통 손실함수(loss function)을 구한 후, loss.backward()를 수행하는데 이는 loss.backward(torch.Tensor([1]))의 shortcut 함수임을 참고하면 사용법을 어느정도 이해할 수 있을 것입니다. 자, 그러면 backward path를 살펴보겠습니다. 시그모이드 함수를 사용해서 우리는 O1과 O2를 생성했습니다. 그러면 시그모이드 함수의 미분값은 어떻게 나와야 할까요? 먼저 시그모이드 함수를 미분할 경우 결과 형태가 $\frac{dsigmoid(x)}{dx} = sigmoid(x)(1-sigmoid(x))$됨은 잘 알려져 있습니다. 즉, $\frac{\partial {O1}}{\partial {s(x)}} = grad_{in} * sigmoid(x)(1-sigmoid(x))$가 됩니다. 이전 forward path에서 시그모이드 입력값이 [1.1059, 1.2249]였기에 이 수식에 대입하면 [0.1868, 0.1755]가 나옵니다. Linear function의 경우도 살펴보겠습니다. 우선 흘러들어온 그래디언트는 이전 시그모이드 레이어의 local gradient [0.1868, 0.1755]입니다. 이 그래디언트가 가중치 매트릭스에 전파되는 수식과 바이어스에 전파되는 수식을 구별해서 살펴봐야합니다. 먼저 본래 수식은 $w*x + b$입니다. 따라서 가중치 매트릭스로 흘러가는 그래디언트는 $\frac{ds(x)}{dw} = grad_{in} * x$입니다. 수식에 대입하면 [0.1868, 0.1755] * [[0.4,0.45],[0.5,0.55]] = [0.1868 * 0.4 + 0.1755 * 0.5, 0.1868 * 0.45 + 0.1755 * 0.55] = [0.1625, 0.1806]입니다. 그런데 이렇게 보면 linear function을 통과했을 때 local gradient 값은 얻어도 linear function의 파라미터 값을 업데이트 시킬 gradient 값은 아직 보지 못했습니다. 사실 register_backward_hook 함수를 이용할 경우 backward path의 그래디언트를 전부 볼 수 있다고 여겼으나 linear function의 정확한 local gradient 값이 나오지 않는 부분은 의문입니다. 이 부분은 추후에 함수 동작을 알게되면 업데이트 하겠습니다.
********* Backward Hooks Inputs & Outputs *********
(tensor([0.0392, 0.0435]), tensor([0.0827]))
(tensor([0.0392, 0.0435]),)
---------------------------------------------------
(tensor([0.0392, 0.0435]),)
(tensor([0.1625, 0.1806]),)
---------------------------------------------------
(tensor([0.1868, 0.1755]), tensor([0.3623]))
(tensor([0.1868, 0.1755]),)
---------------------------------------------------
(tensor([0.1868, 0.1755]),)
(tensor([1., 1.]),)
---------------------------------------------------
편법으로 두번째 레이어의 파라미터 값에 대한 local gradient들을 확인해 보겠습니다. 다음과 같은 코드로 확인해 볼 수 있습니다.
for i in net.fc2.parameters():
print(i.grad)
tensor([[0.1108, 0.1115],
[0.1041, 0.1048]])
tensor([0.3623])
이 결과에서 우리가 수식적으로 풀어낸 결과값을 확인할 수 있습니다. 각 파라미터의 local gradient는 다음과 같이 표현될 수 있습니다.
\[\begin{align} \frac{\partial o_1}{\partial w_1} &= \frac{\partial o_1}{\partial h_1} \frac{\partial h_1}{\partial w_1} \\ &= grad_{in} * sigmoid(h1) * (1-sigmoid(h1)) * x_1 \\ &= 1 * 0.7514 * (1-0.7514) * 0.5933 = 0.1108 \end{align}\] \[\begin{align} \frac{\partial o_1}{\partial w_2} &= \frac{\partial o_1}{\partial h_1} \frac{\partial h_1}{\partial w_2} \\ &= grad_{in} * sigmoid(h1) * (1-sigmoid(h1)) * x_2 \\ &= 1 * 0.7514 * (1-0.7514) * 0.5969 = 0.1115 \end{align}\] \[\begin{align} \frac{\partial o_2}{\partial w_1} &= \frac{\partial o_2}{\partial h_2} \frac{\partial h_2}{\partial w_1} \\ &= grad_{in} * sigmoid(h2) * (1-sigmoid(h2)) * x_1 \\ &= 1 * 0.7729 * (1-0.7729) * 0.5933 = 0.1041 \end{align}\] \[\begin{align} \frac{\partial o_2}{\partial w_2} &= \frac{\partial o_2}{\partial h_2} \frac{\partial h_2}{\partial w_2} \\ &= grad_{in} * sigmoid(h2) * (1-sigmoid(h2)) * x_1 \\ &= 1 * 0.7729 * (1-0.7729) * 0.5969 = 0.1048 \end{align}\] \[\begin{align} \frac{\partial o}{\partial b} &= \frac{\partial o_1}{\partial b} + \frac{\partial o_2}{\partial b} \\ &= \frac{\partial o_1}{\partial h_1} \frac{\partial h_1}{\partial b} + \frac{\partial o_1}{\partial h_2} \frac{\partial h_2}{\partial b} \\ &= (grad_{in} * sigmoid(h1) * (1-sigmoid(h1)) * 1) + (grad_{in} * sigmoid(h2) * (1-sigmoid(h2)) * 1) \\ &= (1 * 0.7514 * (1-0.7514) * 1) + (1 * 0.7729 * (1-0.7729) * 1) = 0.3623 \end{align}\]모든 값들이 일치함을 확인할 수 있습니다. Gradient method 방법이 무엇인지 개념과 동작방식, 구현에 대해 다루었으며 추후 관련된 연구, 업무에 참고가 되길 바랍니다.
Comments